We saw in the chapter related to quizzes that they easily lend themselves to arithmetic exercises. The creation of such "pages" of arithmetic operations can however be a little tedious, so why not use the computer to generate these exercises for you? This is precisely what the arithmetic quiz wizard can do from a simple series of instructions that determine the type of labels you want to obtain. The labels that the wizard generates can be treated as a "first draft" that you can always fine-tune to correspond more closely to what you want to quiz your pupils on. You can also add "distracting" labels (that do not correspond to a good answer) in order to complicate the exercise.
Let's start with a simple example: building an exercise with 24 additions using numbers between 1 and 10. When creating the exercise, you need to choose the "Arithmetic quiz wizard" and then specify the number of arithmetic operations required (24 here), as well as the type of operations ("+" in this case). All other parameters can be left to default.
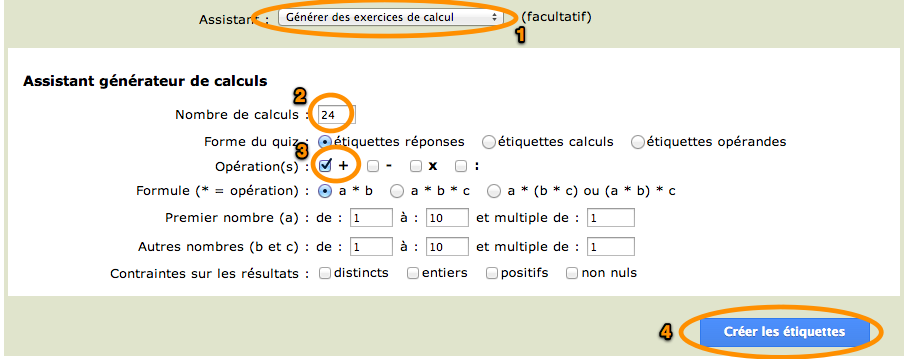
Validating these options by tapping the "Create labels" button will cause the server to build the 24 labels requested, each with an addition, such as the following (only partially displayed here) example:
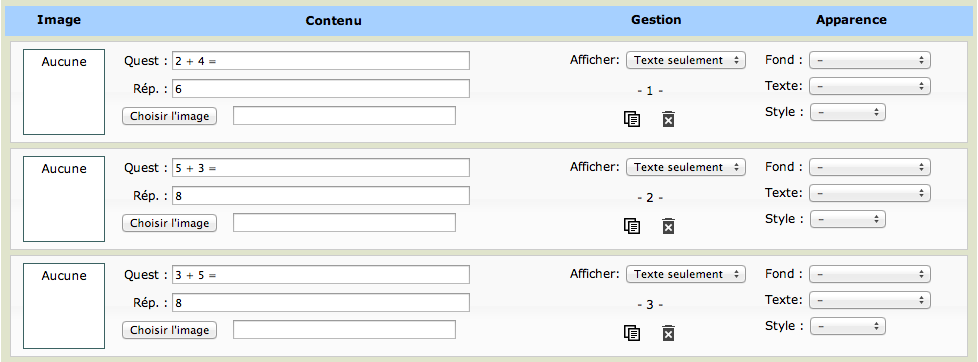
Let's now look in more detail at the different parameters that can be modified to obtain different types of operations as per your own requirements:
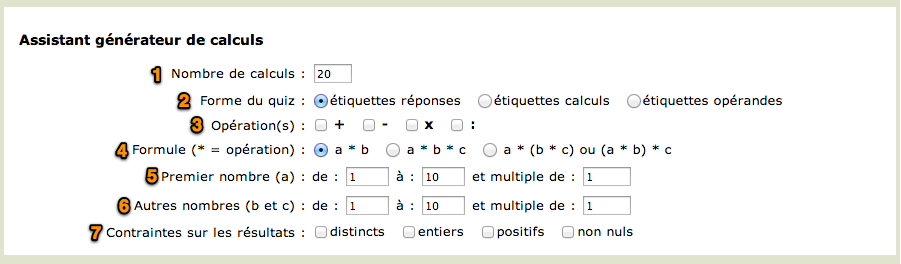
The first of these parameters is self-explanatory: it allows you to specify the number of operations (1) you want to display in the exercise. Note however that if the constraints imposed by the other parameters are too restrictive, this can cause EtiGliss to generate fewer operations than requested. You can also request more operations than required and then chose which ones to keep whilst you delete the rest.
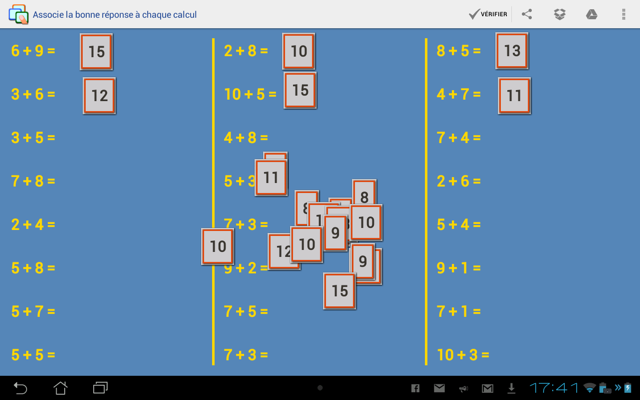
The second parameter determines the quiz format (2) by defining which part of the operation is to be displayed on the labels - and thus constitute the answer to the quiz - and which part will be displayed on the form - and thus represents the question. The example illustrated above uses the most common format whereby the labels hold the result of the operation. It is possible however to generate the opposite exercise where the results of the operations are displayed as the questions, while the labels hold the operations that correspond to these results. The screenshot below shows such an example. When this quiz format is chosen, the results are automatically sorted in ascending order so they can easily be spotted by the pupil, and the option to draw labels one at a time is automatically preselected (but can always be disabled).

The last format available allows to create exercises that ask pupils to find the missing operand of the operation (term or factor) as can be seen below:

The third required parameter of the Arithmetic quiz wizard allows to select the operator(s) (3) to be used in the operations. If you select more than one operator, EtiGliss randomly selects which one will be used for each operation but does not guarantee that the page will include an equal number of operations using each operator.
The fourth parameter "Formula" (4) is used to choose whether the calculation involves two or three operands, and in the latter case, if parenthesis are added or not. It should be noted that in the absence of parenthesis, EtiGliss respects operators priorities, i.e. multiplications and divisions are performed before additions and subtractions. Thus for example 5 x 3 + 2 = 13, since operators priorities require that 5 x 2 = 10 is performed first, followed by 10 + 3 = 13. To prevent confusion and remove any ambiguity, it is customary in primary schools to favor the use of parenthesis.
Parameters (5) and (6) allow to specify which numbers are to be used in the operations, thanks to three indications. The first two are self-explanatory: the minimum and maximum numbers to be used. The third indication is more subtle but very useful: it represents the base of multiplication. The default base is 1 and the numbers obtained, which are multiples of 1, are therefore integers. But changing this value to 10 for example allows to request only multiples of 10, and changing it to 0.1 will limit the values to decimal numbers. Here are some examples of how these parameters can be used:
etc. ..
Finally, the last series of options from the wizard allow you to set some result limiters:
Combining these parameters, we will now generate an exercise containing a mixture of 24 additions and subtractions each using three one-decimal numbers between 1 and 100. Entering these choices in the wizard is done as follows:
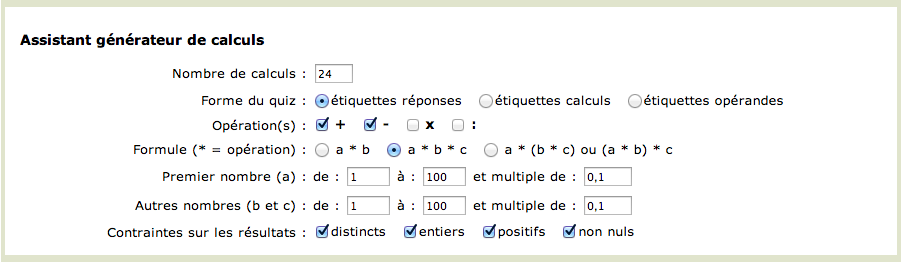
The exercise obtained could look like this:

Admittedly, this wizard cannot model the wealth of exercises that a teacher can design, but it is handy to quickly build a large number of varied operations.
Next document: Managing your preferences